Have you ever gazed at a straight road stretching out before you, only to see another straight road seemingly running parallel beside it? These parallel paths, the very foundation of our understanding of straight lines, are fundamental building blocks in the world of geometry. But what happens when a third line, a transversal, cuts across these parallel paths? Suddenly, a fascinating array of angles emerges, each with its own special relationship to the others. These angles, carefully woven together by the properties of parallel lines, are the subject of a vital concept in geometry known as “two parallel lines cut by a transversal.” Understanding these relationships unlocks a powerful tool for solving a wide range of geometric problems.
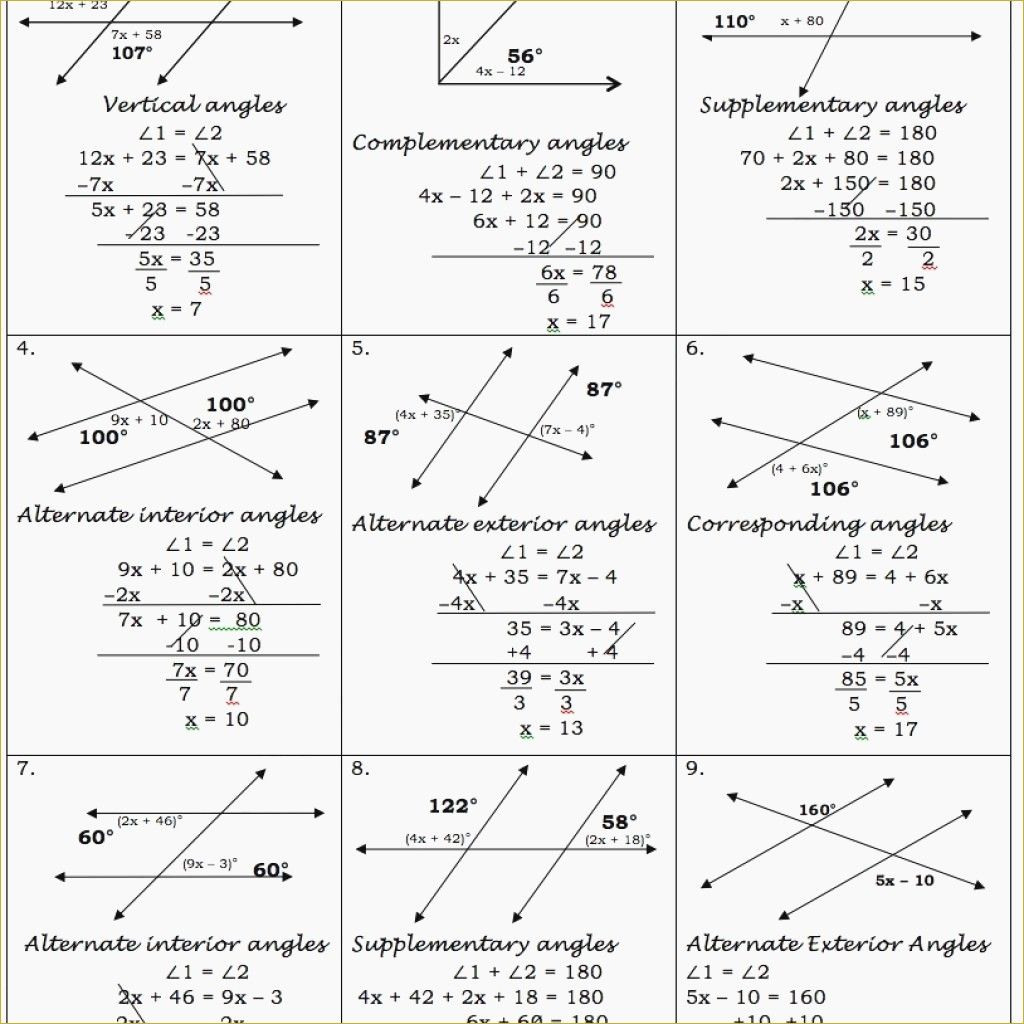
Image: lessondbhoward.z13.web.core.windows.net
This article dives into the world of two parallel lines cut by a transversal, exploring the key concepts, angle relationships, and applications of these powerful geometric relationships. We’ll use clear explanations, practical examples, and a touch of visual flair to help you understand and master the art of these angle relationships. By the end of this exploration, you’ll be equipped with the knowledge to tackle any worksheet, test question, or real-world problem involving two parallel lines cut by a transversal. So, let’s embark on this journey of geometric discovery, together!
Diving into the World of Parallel Lines and Transversals
What are Parallel Lines and Transversals?
Before we delve into the intricate dance of angles, let’s define our key players: parallel lines and transversals.
- Parallel Lines: Imagine two perfectly straight lines extending infinitely in both directions, never meeting, always maintaining the same distance apart. These are parallel lines, represented by the symbol ||.
- Transversal: Now, picture a third straight line that intersects both of our parallel lines. This line is known as the transversal. It’s like a crossroad cutting across the parallel paths, creating a network of angles.
To visualize this, think of railroad tracks. The rails represent parallel lines, while a road crossing the tracks would be a transversal. This simple visual helps us understand the basic relationship between parallel lines and transversals.
The Birth of Special Angle Pairs
The magic happens when a transversal intersects parallel lines. Eight distinct angles are formed at the intersection points, and these angles are not just random measurements. They are meticulously related to each other in specific pairs, forming the foundation of our understanding of parallel lines cut by a transversal.
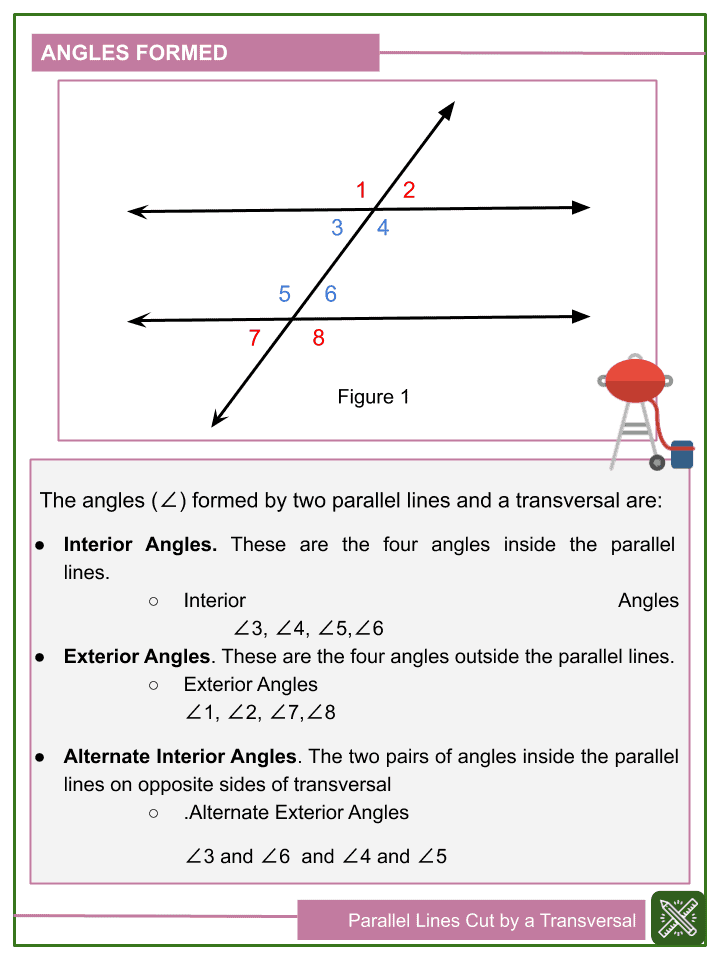
Image: woitowitzleandrosays.blogspot.com
Types of Angle Pairs:
- Corresponding Angles: These angles occupy the same relative position at each intersection point. They are like mirrors, reflecting each other across the transversal.
- Alternate Interior Angles: Imagine a “Z” pattern formed by the transversal and the parallel lines. The angles inside this “Z” pattern, on opposite sides of the transversal, are called alternate interior angles.
- Alternate Exterior Angles: Similar to alternate interior angles, these angles are formed on opposite sides of the transversal, but located outside the parallel lines. Think of a “Z” pattern on the opposite side of the lines.
- Same-Side Interior Angles: These angles lie between the parallel lines and on the same side of the transversal. They are like roommates sharing a space.
The Golden Rule of Parallel Lines Cut by a Transversal
The beauty of parallel lines cut by a transversal lies in a simple but profound rule:
Corresponding Angles are Congruent (Equal in Measure).
This fundamental rule is the foundation for understanding all the other angle relationships within this geometric scenario. Let’s dive deeper into how this rule plays out with the different angle pairs.
Corresponding Angles: The Mirror Images
Imagine an “F” pattern formed by the transversal and the parallel lines. The top two angles of this “F” are corresponding angles. The rule states that they will always be equal. This applies to all corresponding angles formed by the transversal.
Alternate Interior Angles: The “Z” Connection
Recall the “Z” pattern. The angles on opposite sides of the transversal within this “Z” are alternate interior angles. According to the golden rule, these angles are also congruent (equal). This means that if one angle is 70 degrees, the other will also be 70 degrees.
Alternate Exterior Angles: The “Z” on the Other Side
The same “Z” pattern applies to alternate exterior angles, but this time, the “Z” is formed on the outside of the parallel lines. The angles within this “Z” are also congruent, thanks to the magic of the golden rule.
Same-Side Interior Angles: The Supplementary Pair
Unlike the previously mentioned angle pairs, same-side interior angles are not congruent. Instead, they are supplementary, meaning they add up to 180 degrees. This is like two angles sharing a straight line, their measures combining to a total of 180 degrees.
Unlocking the Power of Parallel Lines Cut by a Transversal
Now that we’ve explored the fundamental relationships between angles, let’s see how this knowledge unlocks the door to solving problems and understanding real-world scenarios.
Solving for Unknown Angles
Imagine a diagram of two parallel lines cut by a transversal, where some angles are known and others are unknown. Using the relationships we’ve learned, we can systematically solve for those unknown angles. For example, if we know one corresponding angle is 65 degrees, we immediately know its corresponding angle is also 65 degrees. If we know one alternate interior angle is 110 degrees, the other alternate interior angle must also be 110 degrees. This concept empowers us to solve for any unknown angle within the diagram!
Real-World Applications
Parallel lines cut by a transversal are not just theoretical concepts confined to textbooks—they play a critical role in our world.
- Construction: Carpenters use these concepts to create parallel walls and floors, ensuring everything aligns perfectly.
- Architecture: Architects employ the principles of parallel lines cut by a transversal to design buildings with consistent angles and support structures.
- Navigation: Pilots rely on these geometric relationships to calculate flight paths and maintain precise directions.
- Engineering: Engineers utilize these concepts to design bridges, roads, and other structures, incorporating the strength and stability of parallel lines cut by a transversal.
Mastering the Two Parallel Lines Cut by a Transversal Worksheet Answers PDF
Now, let’s address the topic of the “Two Parallel Lines Cut by a Transversal Worksheet Answers PDF.” These worksheets are valuable resources for practicing and solidifying your understanding of parallel lines cut by a transversal.
Unlocking the Answers: A Step-by-Step Guide
When you are presented with a worksheet, don’t be intimidated by a sea of angles. Approach it systematically, one step at a time:
- Identify the parallel lines: Look for the lines marked with the parallel symbol (||).
- Identify the transversal: Find the line that intersects the two parallel lines.
- Identify the angle pairs: Carefully analyze the relationships between the angles, identifying corresponding angles, alternate interior angles, alternate exterior angles, and same-side interior angles.
- Apply the golden rule: Use the golden rule of corresponding angles being congruent to find the value of unknown angles. Extend this knowledge to solve for alternate interior angles, alternate exterior angles, and same-side interior angles.
- Verify your answers: Double-check your calculations and make sure all your answers are consistent with the rules of parallel lines cut by a transversal.
The Importance of Practice
Practice makes perfect, even when it comes to geometry. Working through various worksheets allows you to solidify the concepts and gain confidence in your ability to apply the principles effectively.
Don’t hesitate to refer to online resources, textbooks, or online tutors for additional support. Engage in collaborative learning with classmates or friends to further enhance your understanding. The more you practice, the more you’ll master the art of parallel lines cut by a transversal!
Two Parallel Lines Cut By A Transversal Worksheet Answers Pdf
Conclusion
Exploring the world of two parallel lines cut by a transversal unveils a fascinating interplay of angles. By understanding the fundamental relationships between angle pairs, we unlock a powerful tool for solving geometric problems and understanding real-world applications. Worksheets provide a valuable platform for practice and reinforcing your knowledge, allowing you to confidently tackle any challenge involving parallel lines and transversals. Embrace the journey of geometric discovery—with dedication and practice, you can master this compelling concept!






