Have you ever wondered how to find the distance between two points on a map or on a coordinate plane? Perhaps you’ve been tasked with navigating a maze, or maybe you’re just curious about the world around you. Whatever the reason, understanding the distance formula can unlock a whole new realm of geometric possibilities.
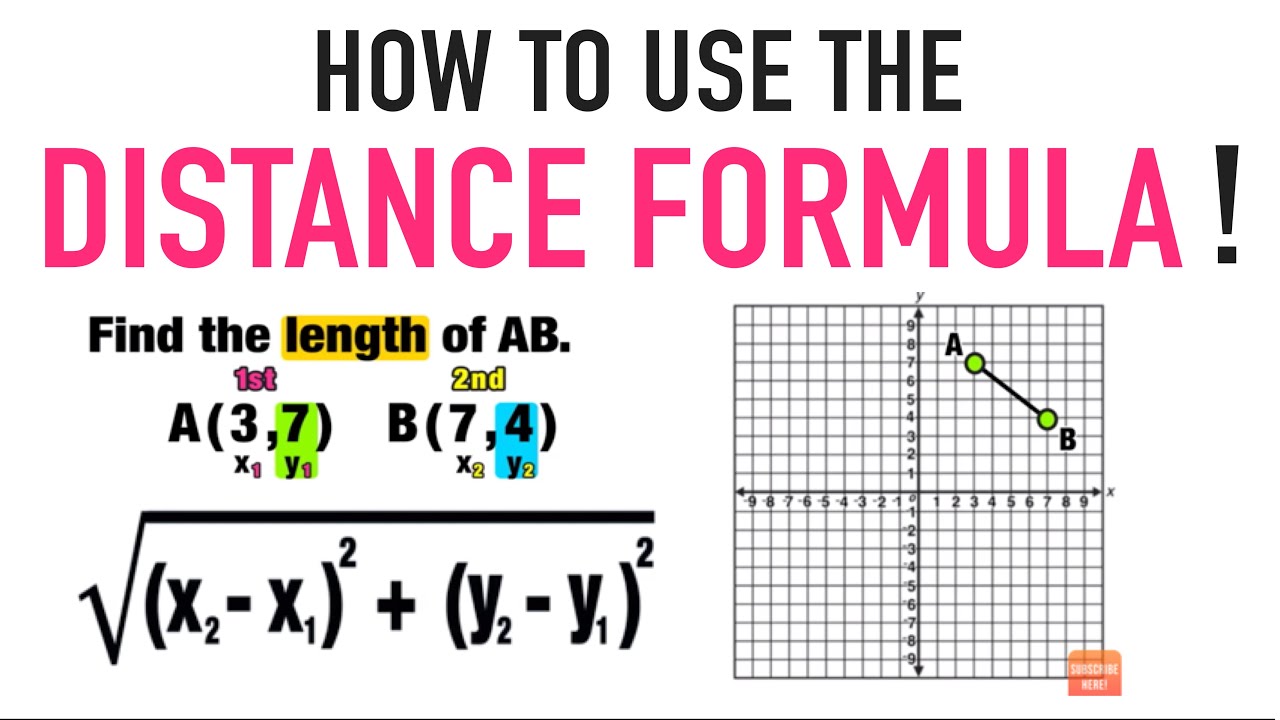
Image: www.youtube.com
The distance formula is a fundamental concept in geometry that allows us to calculate the direct distance between two points in a coordinate plane. It’s a powerful tool that finds applications in countless fields, from architecture and engineering to navigation and computer graphics. By understanding the distance formula and its applications, you’ll gain a deeper appreciation for the beauty and practicality of mathematics.
The History Behind the Distance Formula
To truly understand the significance of the distance formula, it’s helpful to delve into its historical roots. While the concept of distance has been a fundamental aspect of human understanding since ancient times, the formalized expression we know as the distance formula emerged from the development of analytic geometry.
The foundations of analytic geometry were laid by the brilliant French mathematician René Descartes in the 17th century. Descartes’ revolutionary idea was to define geometric objects using algebraic equations. This groundbreaking approach opened up a new world of possibilities for both geometry and algebra, allowing mathematicians to represent and manipulate geometric shapes using numerical values.
The distance formula itself is a natural consequence of applying the Pythagorean theorem to the coordinate plane. The Pythagorean theorem, which states that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse, provides a foundational principle for calculating distances in two-dimensional space.
Understanding the Distance Formula
The distance formula is derived directly from the Pythagorean theorem and represents the general case for calculating the distance between any two points in a coordinate plane. Let’s break down the formula step by step:
The Formula
The distance formula is expressed as follows:
d = √[(x2 – x1)2 + (y2 – y1)2]
Where:
- d represents the distance between the two points.
- (x1, y1) are the coordinates of the first point.
- (x2, y2) are the coordinates of the second point.

Image: www.toppr.com
Visualizing the Formula
To help visualize the distance formula, imagine two points, A and B, on a coordinate plane. Connect points A and B with a straight line segment. This line segment represents the distance between the two points, which we’ll call d. Now, draw a horizontal line segment from point A to a point directly below point B (let’s call this point C). Also draw a vertical line segment from point C to point B. This creates a right triangle with legs of length (x2 – x1) and (y2 – y1) and the hypotenuse equal to d. The distance formula is simply the Pythagorean theorem applied to this right triangle.
Applications of the Distance Formula
The distance formula is a versatile tool with numerous applications across various fields. Here are a few examples:
1. Navigation and Mapping
Distance formulas are fundamental calculations in navigation systems. GPS devices use them to determine the shortest route between two points, taking into account road conditions, traffic, and other factors. In mapping applications, distance formulas are used to calculate distances between cities, landmarks, and points of interest on a map.
2. Computer Graphics
Distance formulas are crucial components in computer graphics. They are used to calculate distances between points, lines, and surfaces for various purposes, such as determining object collision detection, lighting and shading effects, and creating realistic 3D environments.
3. Engineering and Architecture
Engineers and architects utilize distance formulas to design buildings, bridges, roads, and other structures. They need to ensure that these structures are built to scale and meet safety requirements, which often involves calculating distances between various components. For example, they might use distance formulas to calculate the optimal spacing between beams in a building or determine the distances required for safe and efficient vehicular traffic flow on a road.
4. Data Analysis and Statistics
Distance formulas are used in data analysis and statistics to measure the closeness between different data points. This information can be crucial for clustering data into groups, identifying outliers, and understanding relationships between data sets.
Beyond the Basics: Expanding Our Understanding
While the basic distance formula addresses two-dimensional spaces, its concepts extend to more complex dimensions. For example, in three-dimensional space, we can use the distance formula to find the distance between two points with three coordinates each: (x1, y1, z1) and(x2, y2, z2). The formula for three-dimensional space is as follows:
d = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
Understanding the distance formula and its generalizations is paramount for grasping deeper concepts in geometry and related fields.
1.2 4 Journal The Distance Formula
https://youtube.com/watch?v=zdrRE4tfi-M
The Power of a Simple Formula
The distance formula, seemingly a simple equation, holds incredible power. It provides a tool for unlocking the complexities of geometric relationships, enabling calculations that drive advancements in diverse fields.
Whether you’re a student exploring the world of geometry, a professional engineer designing complex structures, or simply someone captivated by the patterns within our world, understanding the distance formula is a valuable asset. Its application extends beyond classroom exercises to shape our understanding and influence our daily lives. So, the next time you encounter a map, a computer-generated image, or even a simple diagram, take a moment to appreciate the elegant and practical power of the distance formula – a mathematical tool that has revolutionized our understanding of the world around us.






